Introducción
Como ya dice el título, este artículo es la continuación
del artículo “el gradiente hidráulico, primera parte”. He intentado explicarlo
lo más visual posible, mediante una serie de ejemplos con figuras, desde
situaciones con un gradiente hidráulico bajo hasta otros con un gradiente mayor
a uno.
Figura 1
Ejemplo 1
Algunos ejemplos de gradiente hidráulico bajo podemos
encontrar en las mesetas del norte de Burgos. Una meseta es una elevación del terreno,
relativamente llana y normalmente de una gran extensión. Estas suelen tener sus
desagües en los barrancos que las rodean. Lo primero que me vienen a mente y
que ha servido como ilustración (figura 2), es el sistema Cueva del
Aguanal-Barbancho/Cueva del Agua. En el Aguanal entra un arroyo a una altura de
956m y el agua sale en la Cueva del Agua (y también por el Barbancho en época
de crecida) en Orbaneja del Castillo a una altura de 736m y a una distancia de
unos 8 km en línea recta. Hoy en día el sistema consiste de una serie de
sifones más o menos cortos y grandes galerías aéreas, pero en su estado inicial
las fisuras deberían haber estado completamente inundadas. En este ejemplo
suponemos que el desarrollo ha sido de un ensanchamiento simultáneo de todas
las fisuras entre A y B (aunque es más probable un desarrollo en fases debido a
la infiltración de precipitación en la meseta).
Figura 2
Lo cual da un gradiente hidráulico inicial máximo de:
i = Δh/L
i = (956-736)/8000
= 220/8000 = 0,0275
Y esto suponiendo una conexión en línea recta, lo cual
obviamente no es así (según las topografías ya realizadas).
Nota: En el
verano de 2019, el espeleobuceador Jason Mallison, en compañía de unos ingleses
y uno de nuestros espeleobuceadores más activos, Pedro González (León), han
llegado hasta el último sifón que separa ambas cuevas.
Ejemplo 2
Unos 11 km al sur de Orbaneja (17 km por carretera) está
el conocido Pozo Azul, situado en los alrededores de Covanera. Se trata de un
manantial importante, situado a una altura de 700 metros y que tiene su área de
recarga a más de 9 km al ESE, medido en línea recta. Entre la zona de recarga
(situada a aprox. 1075m) y el Pozo Azul, la formación calcárea (gris en la
figura 3) está cubierta por margas impermeables (amarilla). Hoy en día la
fisura original se ha desarrollado hasta una amplia cueva que se ha buceado
hasta más de 11 km (además de unos 2 km de galerías laterales alrededor de
Tipperary), sin llegar todavía a la zona de recarga. Por tanto se puede suponer
una distancia mínima de unos 14 km hasta esta zona. Suponiendo un desarrollo de
la cueva embrionaria (wormhole) en una sola fase se puede aproximar el
gradiente hidráulico original.
i = Δh/L
i =
(1075-700)/14000 = 375/14000 = 0,027 (curiosamente casi igual al ejemplo
anterior)
Figura 3
Nota: Es
probable que la altura del manantial se ha disminuida desde la formación de la
cueva embrionaria (Pozo Azul: El porqué de su localización) y que además el
desagüe original haya sido algo más hacia el norte y a una altura algo mayor,
mientras que la altura de la meseta habrá cambiado poco. Esto da una
disminución de Δh y por tanto un
gradiente aún menor. Por otro lado,
las galerías secas de Tipperary indican un desarrollo más complicado.
Nota: Hoy en
día hay poca diferencia en el nivel freático entre el Pozo Azul y la punta de
exploración. Se trata de una situación normal; durante el proceso de desarrollo
de una cueva embrionaria hasta una cueva amplia, llega el momento en que la
recarga puede ser evacuada con tan facilidad, que el gradiente hidráulico se
colapsa.
Ejemplo 3
En las montañas los gradientes hidráulicos suelen ser
mayores. La figura 4 muestra una montaña con una zona vadosa y una zona
freática (saturada con agua), separada por la curva discontinua que representa
el nivel freático. Hay varias fisuras que todavía son estrechas, lo que explica
que el nivel freático todavía no se ha colapsado. El sistema de fisuras desagua
en el punto F.
El gradiente del conjunto de fisuras AB, BC y CF es:
i = Δh/L
i = (hA-hF) / (LAB
+ LBC + LCF) ≈ 0,5
Las dimensiones de la figura 3 son probablemente algo
desproporcionados, con una exageración de la altura, excepto quizás por zonas
con grandes gargantas, como por ejemplo los Picos de Europa.
Figura 4
Ejemplo 4
Este ejemplo
trata el gradiente hidráulico en las fisuras de la zona vadosa. Como el flujo
en esta zona es principalmente subvertical, suponemos que en este ejemplo las
fisuras estrechas son verticales (figura 5). También suponemos que las 3
fisuras estrechas (pero no muy estrechas) se han llenado con agua porque está
lloviendo y porque el epikarst concentra la precipitación hacia ellas.
El gradiente
hidráulico de la fisura A es 1, porque la diferencia en altura ΔhA es igual a su
longitud. Lo que pasa es que está fisura se pierde en la profundidad (o cambia
de estrecha a muy estrecha). El resultado es que una vez que se haya llenado,
el flujo tiene una velocidad mínima (se dispersa en fisuras muy estrechas) y
además está prácticamente saturado. Esta fisura se ensancha muy lentamente. Lo
cual pone de manifiesta que aunque el gradiente hidráulico es un factor importante,
no es el único. En este caso el diámetro y la interconexión de las fisuras son
más importantes.
También el
gradiente hidráulico de la fisura B
es 1, pero en este caso el flujo
termina en el techo de una cueva vadosa. En este caso la longitud de la fisura
no tiene importancia (respecto al gradiente, si respecto al tiempo de ruptura),
porque mientras está llena el gradiente hidráulico sigue siendo 1. La cantidad de agua que baja por la
fisura depende principalmente de su diámetro. El ensanchamiento de la fisura
depende principalmente de la cantidad y la composición del agua que pasa por
ella y de la composición de la propia roca.
El gradiente de
la fisura C es algo menor de 1, porque la Δh es algo menor que su longitud. Esto es debido a que la parte
inferior de la fisura se encuentra en la zona freática, es decir por debajo del
nivel freático. También esta fisura termina en el techo de la cueva (ahora
freática) y su situación es muy parecida a la de la fisura B.
Figura
5
Ejemplo 5
Este ejemplo de un gradiente hidraulico alto puede causar pérdidas
de agua alrededor de un muro de un embalse. La figura 1 muestra una fisura F situada hacia la base del muro y que está conectada con el
pantano. Su Δh es casi igual a la
profundidad del pantano a otro lado del muro. Su longitud será un poco más que
la anchura del muro, es decir mucho menor que Δh. Situaciones como estas pueden representar problemas graves,
tanto de seguridad como de pérdida de agua acumulada.
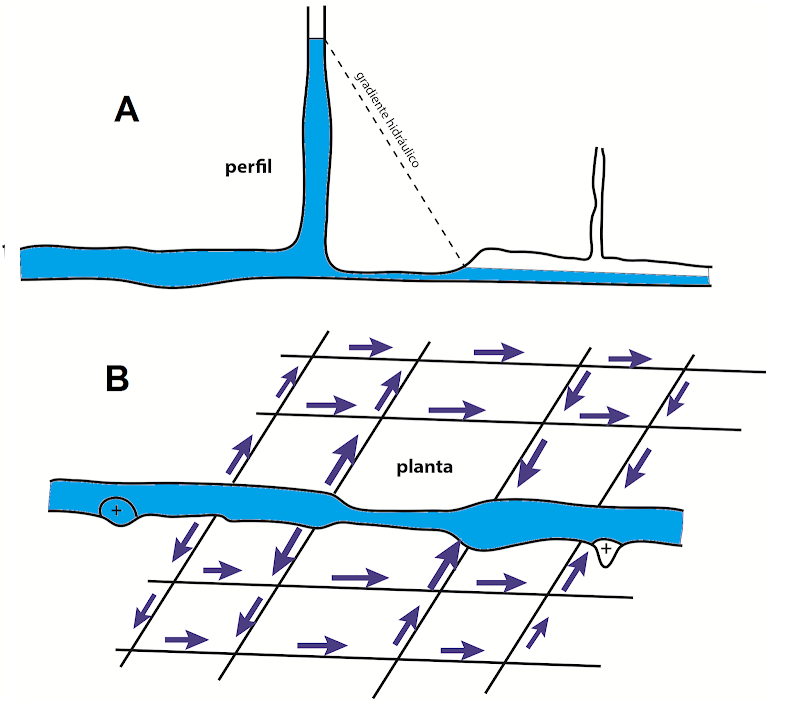
Ejemplo 6
La figura 6A muestra otro ejemplo de un gradiente
hidraulico bastante mayor que 1. Se
trata de un estrechamiento pronunciado en una cueva. Puede ser por un tramo de
roca más resistente a la disolución y/o erosión mecánica, o quizás por un
derrumbamiento. Nos imaginamos una crecida. El caudal se multiplica, pero el
estrechamiento no deja pasarlo por completo. El agua se acumula delante del
estrechamiento. Con el aumenta de la altura del nivel de agua también aumenta
la cabeza de presión hidraulico, lo cual “empuja” más agua por el estrechamiento.
En algún momento se llega a un equilibrio (figura 5A). El gradiente hidraulico
depende de la cabeza de presión (altura de la columna de agua) y de la longitud
del estrechamiento. Las subidas del nivel de agua puede ser muy considerables,
como por ejemplo los 196 metros en el SistemaRepublicano-Cabito. Por tanto es muy posible que durante las crecidas, en
algunas cuevas existen gradientes hidraulicos superior a 5.
Un indicio de que algunas cuevas han experimentado gradientes
hidraulico grandes en su pasado es la presencia actual de sectores con galerías
laberínticas. Hipótesis descrita por Arthur Palmer en 1975 (The originof maze caves).
La figura 6B muestra la misma situación, pero ahora visto en
planta. La gran cabeza de presión y la corta longitud de las fisuras resultan
en un gradiente hidraulico grande. Hay un flujo importante en todas las fisuras
y todas se ensanchan rapidamente. En este caso se pueden desarrollar varios
conductos alrededor del estrechamiento, que finalmente resulta en un sector
laberíntico. Al revés podemos deducir que la presencia de sectores
laberínticos, especialmente si se puede localizar el estrechamiento, indican un
gran gradiente hidraulico en su origen.
Nota: el aumento de la velocidad con que una
fisura se ensancha, debido a un aumento del caudal (y eventual disminución de
la saturación), no es continua, pero que después de un máximo llega a disminuir
para finalmente parar. A partir de este momento la velocidad con que un conducto se ensancha es constante y máxima, y
puede tener un valor de alrededor de 0,1mm al año o un poco más.
La consequencia es que en el caso de la figura 6B, todas
las fisuras que llegan a ensancharse a una velocidad máxima se pueden convertir
en galería. Una vez que el caudal es suficiente para establecer un crecimiento
máximo, su importancia es mucho menor.
.







No hay comentarios:
Publicar un comentario